We are Mechatronic Innovators! Contact Us
Heat Transfer
BACK TO OVERVIEW
Introduction
In engineering, thermal stability is crucial to ensuring the dimensional stability of a system. Heat transfer plays a crucial role in this context. Effectively managing heat transfer and isolating any thermal loads is important, as they can lead to thermal expansion or contraction of materials, potentially compromising the accuracy of your system. Actuators, friction, light, environmental temperature, and even the presence of a person are all examples of heat loads that may impact the performance of your machine.
There are three types of heat transfer: conduction, convection, and radiation.
Conduction
Conduction is the transfer of heat through a solid material from a higher temperature region to a lower temperature region. It’s governed by Fourier’s Law, which states that the heat transfer rate through a material is proportional to the negative gradient of the temperature and the area perpendicular to the heat transfer direction. The mathematical representation is given by:
\dot{Q}=-kA\dfrac{dT}{dx}
where \dot{Q} is the heat transfer rate (W), k is the thermal conductivity of the material (W/m·K), A is the cross-sectional area perpendicular to the direction of heat transfer (m²), and dT/dx is the temperature gradient in the direction of transfer (K/m). Materials with a high conductivity are copper and aluminum, while materials with a low conductivity (isolators) are PEEK and Zerodur.
Convection
Convection involves the transfer of heat between a solid surface and a fluid (liquid or gas) moving over it. The rate of convective heat transfer is described by Newton’s law of cooling:
\dot{Q}=hA(T_s-T_f)
where h is the convective heat transfer coefficient (W/m²·K), T_s is the surface temperature (K), and T_f is the fluid temperature (K).
Convection can be classified into two main types:
- Natural Convection: This occurs when the fluid motion is caused by buoyancy forces that are induced by density differences due to the variation in temperature in the fluid. For example, warmer parts of a liquid or gas rise because they are less dense, while cooler parts sink because they are denser. The value of h for air is typically between 5 and 25 W/m²·K for natural convection.
- Forced Convection: In this type, the fluid is forced to flow over a surface or in a tube by external means such as a fan, pump, or wind. The movement is not caused by density differences but by external mechanical means such as the down flow in a clean room. The value of h for air is typically between 10 and 200 W/m²·K for forced convection.
The convective heat transfer coefficient for air flow can be approximated to:
h = 12.12 – 1.16 \; v \; + \; 11.6\; \sqrt{v}
where v is the relative speed between the surface and air. Note: this is an empirical equation for velocities between 2 to 20 m/s.
Radiation
Radiation is the transfer of energy by electromagnetic waves and does not require a medium to propagate. The Stefan-Boltzmann law describes the power radiated from a black body in terms of its temperature:
\dot{Q}=\sigma \varepsilon A(T_c^{4}-T_0^{4})
where \sigma is the Stefan-Boltzmann constant, \varepsilon is the emissivity of the surface, T_c is the temperature of the component emitting the radiative heat and T_0 is the ambient temperature (K). From the formula above it is clear that radiation is only noticeable when the temperature difference is significant.
Emissivity is a measure of a material’s ability to emit energy as thermal radiation compared to that of a perfect black body at the same temperature. It is a dimensionless quantity, ranging from 0 to 1, where 1 represents perfect emission akin to a black body. The emissivity of a material affects how efficiently it can radiate heat into its surroundings and is dependent on its color, temperature and reflectivity. Gold has a low emissivity and is typically used in cryogenic applications to minimize radiation.
Specific heat
The specific heat is the amount of heat per unit mass required to raise the temperature by one degree Celsius. It’s crucial for understanding how much heat energy is needed for a material to undergo a temperature change:
Q=m c_p \Delta T
where Q is the heat energy (J), m is the mass (kg), c_p is the specific heat capacity (J/kg·K), and \Delta T is the temperature change (K).
Thermal resistance
An analogy exists between the diffusion of heat and electrical charge. Just as an electrical resistance is associated with the conduction of electricity, a thermal resistance may be associated with the conduction of heat. Defining resistance as the ratio of a driving potential to the corresponding transfer rate, it follows from \dot{Q}_{cond} that the thermal resistance for conduction is:
R_{cond}\equiv\dfrac{dT}{\dot{Q}_{cond}}=\dfrac{L}{kA}
A thermal resistance may also be associated with heat transfer by convection at a surface, namely:
R_{conv}\equiv\dfrac{T_s-T_f}{\dot{Q}_{conv}}=\dfrac{1}{hA}
Circuit representations provide a useful tool for both conceptualizing and quantifying heat transfer problems such as composite walls or systems. Such walls may involve any number of series and parallel thermal resistances due to layers of different materials. Consider the series composite wall in the figure below.
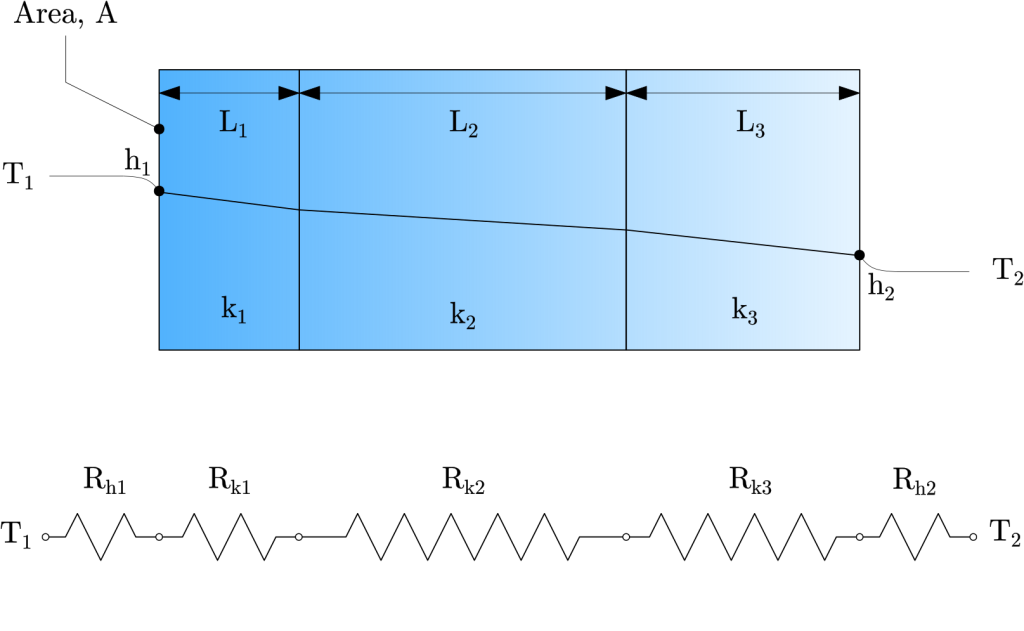
The one dimensional heat transfer rate for this system may be expressed as:
\dot{Q}=\dfrac{\Delta T}{\sum R_t}
in which the total thermal resistance for the components in series are calculated as:
R_{t,series}=\sum_{i=1}^{n}R_i=R_1+R_2+…+R_n
As mentioned, composite walls may also be characterized by series–parallel configurations. The total thermal resistance for the components in parallel are calculated as:
R_{t,parallel}=\dfrac{1}{\sum_{i=1}^{n}\dfrac{1}{R_i}}=\dfrac{1}{\dfrac{1}{R_1}+\dfrac{1}{R_2}+…+\dfrac{1}{R_n}}
Contact resistance
It’s important to acknowledge that in composite systems, the temperature difference at the interface between two materials can be significant. This change in temperature is due to what is referred to as the thermal contact resistance R_{tc}. The thermal contact resistance is influenced by the surface roughness, material properties, and the pressure applied to the contact surfaces. It’s given by:
R_{tc}=\dfrac{1}{h_{c}A}
where R_{tc} is the thermal contact resistance (K/W), h_c is the thermal contact conductance (W/m²·K), and A is the contact area (m²).
The thermal contact conductance is a critical parameter in defining R_{tc}. Theories such as Mikic’s correlation have been developed for calculating h_c. However, the most reliable results are those that have been obtained experimentally.
Vacuum and Cryogenic Environments
Vacuum: convection is negligible in vacuum as there is virtually no medium to transfer the heat.
Cryogenic temperatures: At cryogenic temperatures, materials exhibit different thermal properties, such as increased thermal conductivity or specific heat. Such conditions demands an in-depth understanding of these properties and their impact on heat transfer.
