Two parallel leaf springs

Introduction

Flexure mechanisms, such as leaf springs, have gained prominence in applications where the absence of play, friction and hysteresis are essential. Unlike traditional mechanical joints with bearings, flexure mechanisms eliminate the need for lubrication and the associated wear and friction, resulting in superior reliability and long-term precision. Flexures are typically designed to be compliant along specific axes or directions, allowing controlled deformation or motion in those directions while remaining stiff in the other directions. Flexure mechanisms can replace hinges for limited angular motion and linear guides for limited linear strokes.

To achieve a linear guide with rotational stiffness, two parallel leaf springs can be used as they facilitate parallel displacements and even offer an quasi straight guiding over a relatively small stroke.

Two parallel leaf springs
Shortening effect

A disadvantage of two parallel leaf springs is the shortening effect \Delta y. This shortening effect is a direct consequence of the compliance inherent in flexure mechanisms. As they undergo lateral displacement \Delta x, the individual flexures flex and deform, causing a reduction in their effective length. This parasitic movement in the negative y-direction is most of the times unwanted as it results in a quasi straight guiding.

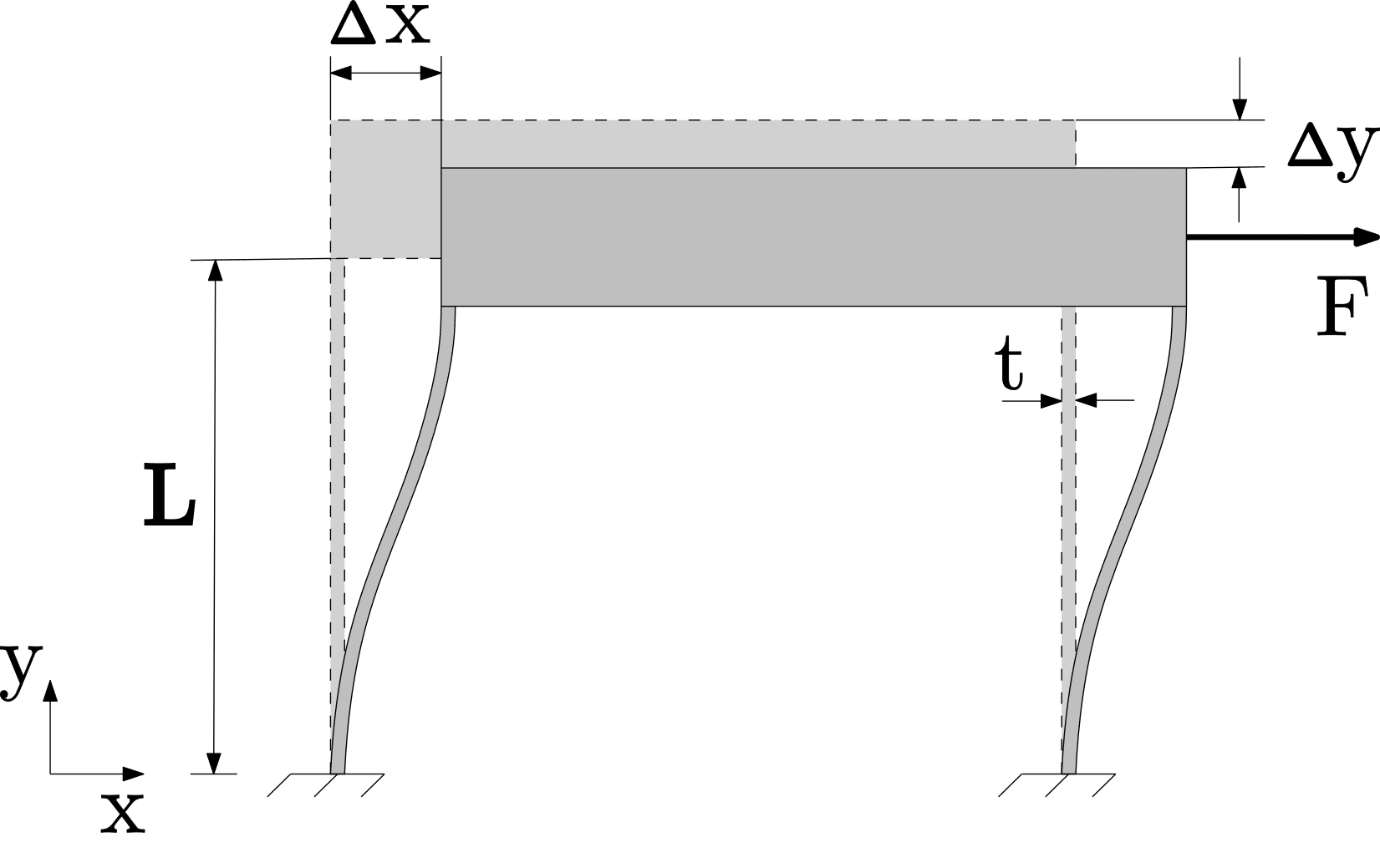
Two parallel leaf springs

For small movements in x-direction the shortening effect \Delta y can be approximated by:

\Delta y = -0.6 \dfrac{(\Delta x)^2}{L}

Stiffness

The stiffness of a parallel leaf spring guiding, with width w, is low in the direction of movement and high in the other two directions, i.e.:

c_x = 24 \dfrac{EI}{L^3} = 2 \dfrac{Ewt^3}{L^3}

c_y = 2 \dfrac{EA}{L} = 2 \dfrac{Ewt}{L} if \Delta x = 0

c_y = 350 \dfrac{Ewt^3}{(175t^2 + 3 \Delta x^2)L} if \Delta x \neq 0

c_z = 6 \dfrac{EI}{L^3} =  \dfrac{Ew^3t}{2L^3}

Stress

The maximum bending stress due to a translation \Delta x in both leaf springs ends is:

\sigma = \dfrac{3Et \Delta x}{L^2}

Calculator
Parallel leaf spring

Input

mm
mm
mm
GPa
mm

Result

mu
N/m
N/m
N/m
N/m
MPa

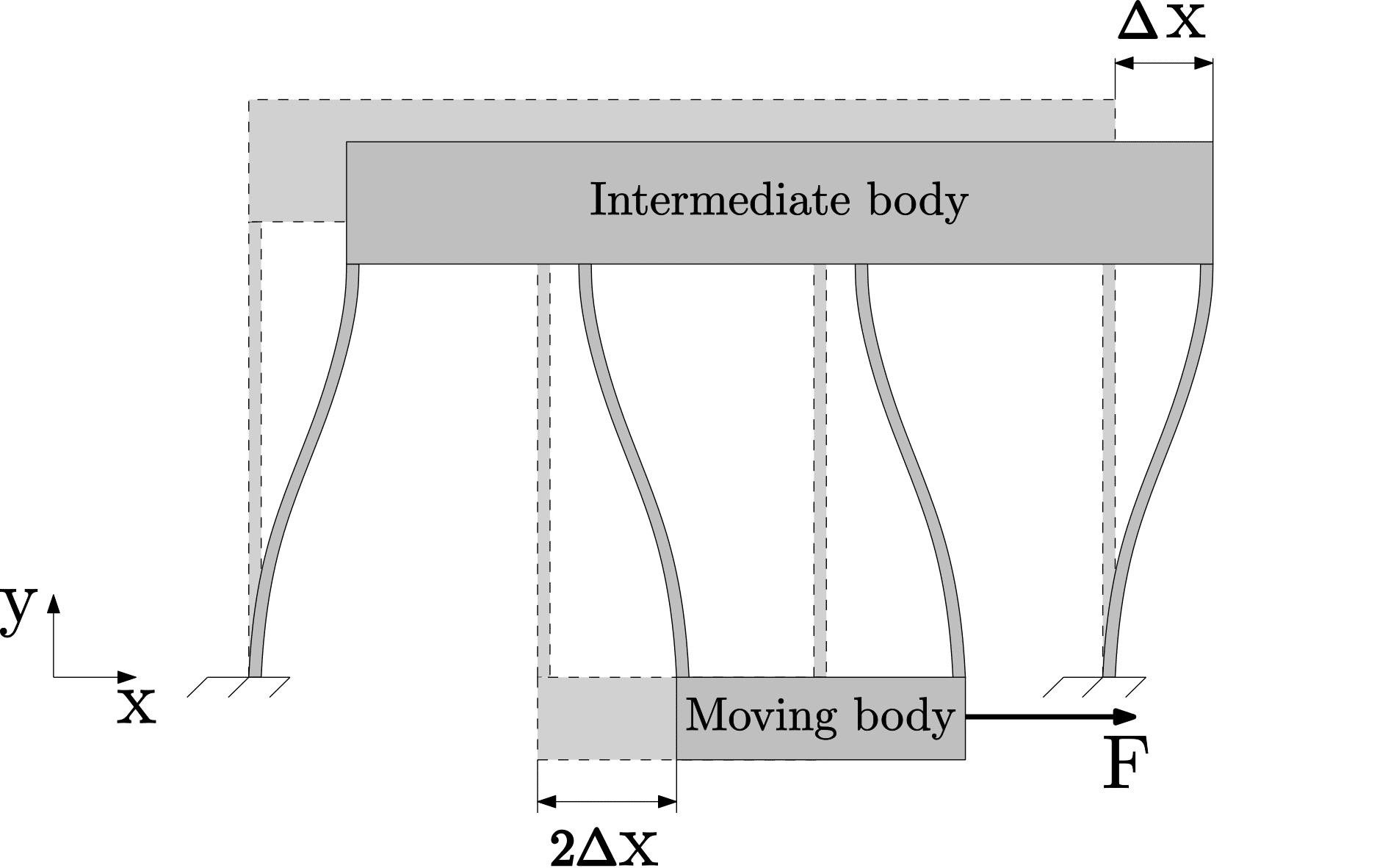
Compensating the shortening effect

The shortening effect \Delta y, which is a parasitic displacement, can be compensated or eliminated through a double parallelogram flexure mechanism as shown below. A double parallelogram flexure is a mechanical structure composed of two sets of parallel leaf springs arranged in series, with each set consisting of two parallel leaf springs. Both sets of parallel leaf springs are connected by an intermediate body, while one set is attached to the moving body within the mechanism. When the moving body displaces in the x-direction, the intermediate body also moves, but its displacement is only half that of the moving body.

The shortening effect of the double parallelogram flexure is eliminated through the unique arrangement of the parallel leaf springs and the intermediate body. In this configuration, when the moving body is displaced, one set of parallel leaf springs experiences a shortening effect in the positive x-direction, while the other set undergoes the same shortening effect but in the negative x-direction. As a result, the moving body moves along a straight line. This behavior is achieved only when the motion of both bodies satisfies the proper displacement ratio of 1:2.

However, a disadvantage of the double parallelogram flexure is the low eigen-frequency of the intermediate body. This can be addressed by connecting the intermediate body to the moving body via a rotating lever arm, ensuring a 1:2 displacement ratio between them. However, this solution may lead to a larger footprint.

Double parallelogram flexure mechanism
Back to overview

NEED TECHNICAL SUPPORT?

Contact Us